Plotting this function in the range π₯ β produces the graph below, which we could verify by creating a table of values or by using any standard graph-plotting software. This function has two roots that can be found by factoring or by the quadratic root formula as π₯ = 1 and π₯ = 3. We will demonstrate both of these types of reflections using an example quadratic function. Similar working shows that the same result holds when reflecting a function twice in the π¦-axis. If we were then to reflect π ( π₯ ) in the π₯-axis to obtain a new function β ( π₯ ), then we would find that β ( π₯ ) = β π ( π₯ ) = β ( β π ( π₯ ) ) = π ( π₯ ), thus returning the original function, as expected. Using the definition would give π ( π₯ ) = β π ( π₯ ). Suppose we took some function π ( π₯ ) and reflected in the π₯-axis to obtain π ( π₯ ). We can see that this property is respected by the algebraic rules that were set out in the definition above.
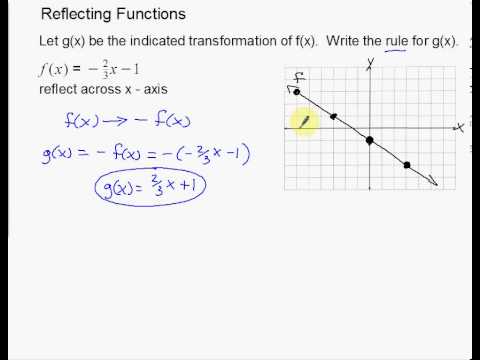
The argument would similarly hold for a double reflection in the π¦-axis. For example, we would expect that if we were to reflect a function π ( π₯ ) in the π₯-axis and then reflect the new function again in the π₯-axis, then we would recover the original function. Then, a reflection in the π₯-axis can be produced using the function π¦ = β π ( π₯ ), and a reflection in the π¦-axis can be found using the function π¦ = π ( β π₯ ).Δͺs an aside, we might ask to verify the above definition with a simple check.
As we will see, these two types of reflections are simple to understand visually, and have a similarly straightforward algebraic interpretation.Δefinition: Reflecting a Function in the Horizontal or Vertical AxisΔ¬onsider a function π¦ = π ( π₯ ) that is plotted on the standard π₯ π¦-axis. These can all be understood algebraically as well as visually, although the simplest case is the reflection in either of the axes. It is possible to reflect any function through any straight line, such as the line π¦ = π₯ or any other of the form π¦ = π π₯ + π. This explainer will focus on what happens to a graph when it is reflected in the π₯-axis or π¦-axis. Fortunately, many transformations are simple to explain using intuitive algebraic rules, especially for some types of translations, reflections, and dilations. Given that a function is ideally written as a formula or an algebraic expression, it is a natural extension to ask how transforming the function can be represented within this framework. If a function is well-defined (either algebraically or with a suitably descriptive graph), then its qualitative behavior can be known at all points, and we might then be interested in how the function behaves when it is subjected to various transformations. In many senses, understanding the effects of transformation on a function can be thought of as a generalization of the above approach. Approaching the topic in such a way will allow for a visual understanding of transformations to be combined with concepts that are drawn from coordinate geometry. A common way of illustrating this is to refer to the vertices of a shape, which can be expressed using precise coordinates and hence can have these movements tracked as the result of transformations being applied. Once these notions are understood intuitively, it is common to begin treating the subject a little more precisely, with the aim of understanding exactly what happens to a shape when it undergoes some combination of transformations.
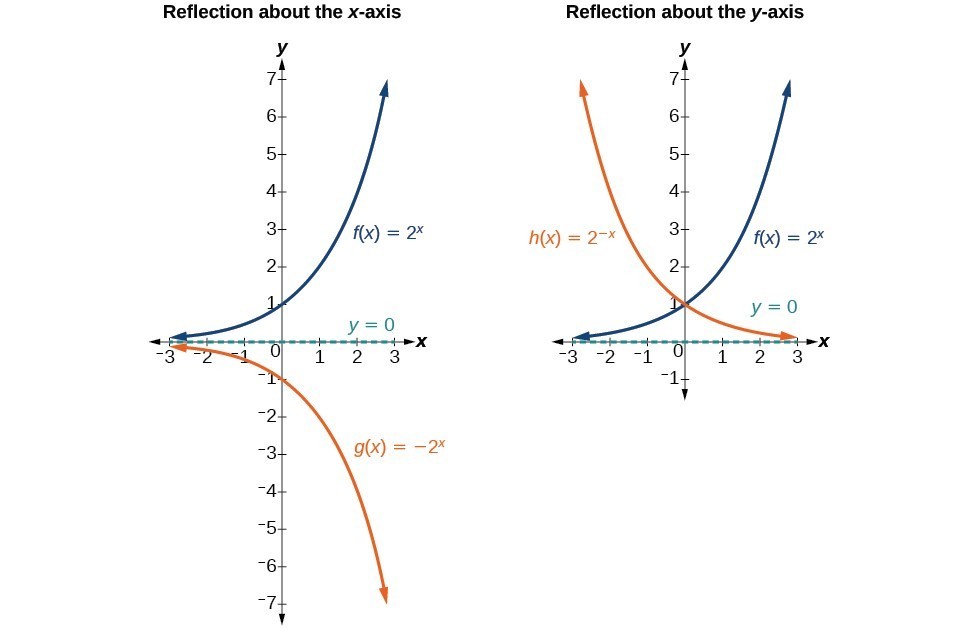
Often, these concepts are illustrated using polygons and other common concepts, usually with familiar and ubiquitous shapes, such as triangles and circles. One of the fundamental concepts in geometry is that of transforming a shape with the standard actions of translation, rotation, reflection, and dilation.
REFLECTION IN Y AXIS EQUATION HOW TO
In this explainer, we will learn how to reflect a graph on the π₯- or π¦-axis, both graphically and algebraically.
0 kommentar(er)
