

Geometric series converge and have a sum to infinity if |r|<1. The series converges because the terms are getting smaller in magnitude. Therefore the fractions will fill an area of. The series converges to a final value.įor example, in the series, the fractions can be seen to fit inside the area of a 1 by 1 square. This means that the terms being added to the total sum get increasingly small. If |r|<1, the sequence will converge to the sum to infinity given by S ∞=a/(1-r).Ī convergent geometric series is one in which the terms get smaller and smaller. If the common ratio is outside of this range, then the series will diverge and the sum to infinity will not exist.

The sum to infinity only exists if -1
SUM OF GEOMETRIC SEQUENCE ONLINE HOW TO
How to Find the Sum to Infinity of a Geometric Series This means that the sequence sum will approach a value of 8 but never quite get there. The sum of an infinite number of terms of this series is 8. The sum to infinity of the series is calculated by, where is the first term and r is the ratio between each term.įor this series, where and, which becomes. We can see that the sum is approaching 8.Įventually, if an infinite number of terms could be added, the sum would indeed approach 8. īecause the terms are getting smaller and smaller, as we add more terms, we are adding an increasingly negligible amount. If the first term is zero, then geometric progression will not take place.As more terms are added, we see that, , and.

Q 6: Can zero be a part of a geometric series?Ī: No. While a geometric sequence is one where the ratio between two consecutive terms is constant. An arithmetic sequence is one where the difference between two consecutive terms is constant. Q 5: Explain the difference between geometric progression and arithmetic progression?Ī: A sequence refers to a set of numbers arranged in some specific order. Here a 1 is the first term and r is the common ratio. Q 4: What is the formula to determine the sum in infinite geometric progression?Ī: To find the sum of an infinite geometric series that contains ratios with an absolute value less than one, the formula is S=a 1/(1−r). For example, the sequence 2, 4, 8, 16 … is a geometric sequence with common ratio 2. Q 3: Explain what do you understand by geometric progression with example?Ī: A geometric progression (GP) is a sequence of terms which differ from each other by a common ratio. Substituting values in the equation we get n = 5 Sum of n terms of GP is a * (r n – 1)/ (r – 1) Q 2: How many terms of the series 1 + 3+ 9+…. If the first, third and fourth terms are in G.P then? If y² = xz, then the three non-zero terms x, y and z are in G.P.If all the terms in a G.P are raised to the same power, then the new series is also in G.P.Reciprocal of all the terms in G.P also form a G.P.If we multiply or divide a non zero quantity to each term of the G.P, then the resulting sequence is also in G.P with the same common difference.Here n is the number of terms, a 1 is the first term and r is the common ratio. To find the sum of first n term of a GP we use the following formula: So, \( \frac \) Geometric Progression Sum So, what do you think is happening? Can we say that the ratio of the two consecutive terms in the geometric series is constant?
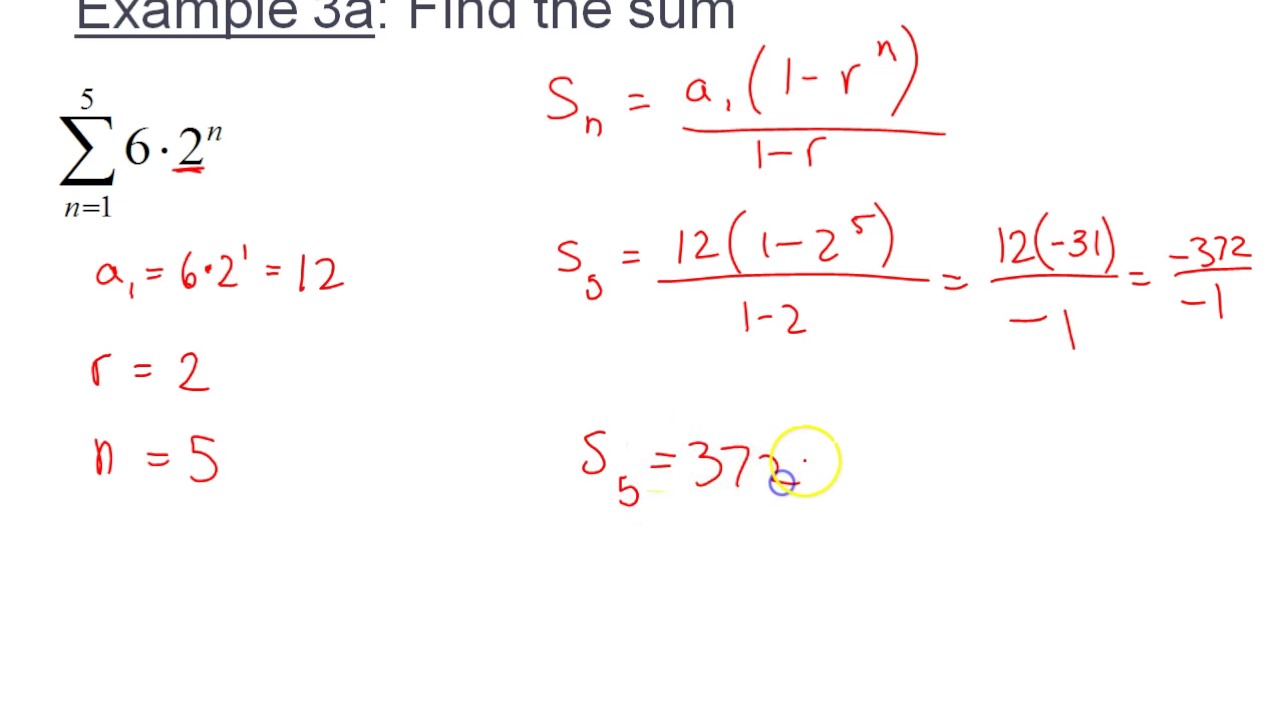
Likewise, when 4 is multiplied by 2 we get 8 and so on. In other words, when 1 is multiplied by 2 it results in 2. Here the succeeding number in the series is the double of its preceding number. For example, the sequence 1, 2, 4, 8, 16, 32… is a geometric sequence with a common ratio of r = 2. A geometric progression is a sequence in which any element after the first is obtained by multiplying the preceding element by a constant called the common ratio which is denoted by r.


 0 kommentar(er)
0 kommentar(er)
